So sánh lãi đơn và lãi kép

Posted by nguyenthucvuhoang

I, Đặt vấn đề
Hầu như bất kỳ một sinh viên nào (ít nhất thuộc khối ngành kinh tế) đều đã từng được làm quen với khái niệm lãi đơn và lãi kép.Hiểu đơn giản đó là giả sử ta gửi tiết kiệm 1,000$ vào ngân hàng vào ngày hôm nay, đến khi ta rút số tiền đó ra thì hẳn nhiên sẽ là một số tiền lớn hơn 1,000$ ban đầu bao gồm tiền gốc 1,000$ và lãi từ 1,000$ đô đó. (phần lãi này có thể hiểu nôm na, xem như là chi phí cơ hội hoặc cũng có thể coi là chi phí sử dụng vốn mà ngân hàng trả cho chúng ta, ở đây chúng ta đang trong vai trò người đầu tư, người cho vay và ngân hàng là người đi vay – mục đích là huy động vốn, họ sẽ dùng số tiền đó để tái đầu tư và thu lại được một khoản lợi nhuận khác… Tương tự trong các tình huống khác, chứ không nhất thiết là gửi tiết kiệm).
Khái niệm lãi đơn hiểu đơn giản là phần lãi sẽ chỉ tính từ vốn gốc ban đầu, trong khi lãi kép cứ sau mỗi một kỳ sẽ được cộng dồn phần lãi với phần gốc rồi tính lãi dựa trên phần tính lãi mới đó. Câu hỏi đặt ra là ta nên tính theo loại lãi nào để thu được lợi ích lớn nhất? ( Mặc dù trong thực tế lãi kép được sử dụng phổ biến chứ không phải là lãi đơn)
Chúng ta sẽ xem xét mối quan hệ giữa lãi đơn và lãi kép trong ngắn hạn cũng như dài hạn trong bài viết này để làm rõ đối với mức thời gian đáo hạn nào thì sử dụng loại lãi nào sẽ mang lại lớn ích lớn hơn. Mặc dù đây không phải là một tính chất quan trọng của Toán Tài Chính (quan trọng ở đây được hiểu theo nghĩa là nó có những ứng dụng đáng kể trong lĩnh vực này) nhưng nó là một tính chất rất cơ bản mà người học nhập môn TTC nên biết. Đây cũng là lời giải của mình cho một bài tập trên lớp, môn Toán Tài Chính 1 – Đại học Kinh tế Tp HCM.
Trước hết ta nhắc lại công thức tính của 2 loại lãi suất này.

Công thức tính lãi đơn như sau: $\displaystyle A_1 = X(1 + t \times i)$

Công thức tính lãi kép như sau: 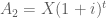$\displaystyle A_2 = X(1 + i)^t$

Trong đó:

$\displaystyle X$ là khoản tiền bỏ ra đầu tư (ví dụ như một khoản tiền gửi ngân hàng – deposit).
$\displaystyle i$ là mức lãi suất thoả thuận.
$\displaystyle t$ là thời gian nhận lại khoản tiền bao gồm cả vốn lẫn lãi.

Các biến này có miền xác định như sau: $\displaystyle X,i,t \in \mathbb{R^+}$ hay $\displaystyle X,i,t \in (0;+\infty)$
Câu hỏi đặt ra là giá trị của $\displaystyle A_1$ và $\displaystyle A_2$ sẽ có quan hệ như thế nào với thời gian nhận lại khoản tiền đầu tư t.

$\displaystyle \triangledown$

II. Một số lời giải
Ta xét hai khoảng thời gian để so sánh $\displaystyle A_1$ và $\displaystyle A_2$ . Dễ thấy trong ngắn hạn (dưới 1 năm) thì $\displaystyle 0<t<1$ , trong dài hạn (trên một năm) thì $\displaystyle t>1$ . Hiển nhiên khi $\displaystyle t=1$ thì $\displaystyle A_1=A_2$ . Do $\displaystyle X>0$ nên để so sánh $\displaystyle A_1$ và $\displaystyle A_2$ ta chỉ cần xét hàm sau là đủ:

$\displaystyle f(i,t)=(1 + i)^t-(1 + t \times i)$

Cố định biến $\displaystyle t$ ta xét đạo hàm hàm $\displaystyle f(i,t)$ theo $\displaystyle i$ khi đó: (Điều này hiệu quả hơn là nếu cố định $\displaystyle i$ và lấy đạo hàm theo $\displaystyle t$ khi đó lời giải sẽ khó hơn nhiều vì đạo hàm của hàm mũ khá phức tạp)
$\displaystyle f(i,t)=f(i)\Rightarrow \left\{\begin{matrix} f'(i)=t(1+i)^{t-1}-t \\ f''(i)=t(t-1)(1+i)^{t-2} \end{matrix}\right.$
Ta xét hai trường hợp sau:
$\displaystyle \triangleright$ Trường hợp 1: Nếu $\displaystyle t>1$ khi đó dễ thấy $\displaystyle f''(i)>0$ do đó $\displaystyle f'(i)$ là một hàm đồng biến. Mặt khác lại có $\displaystyle i>0$ cho nên:

$\displaystyle f'(i)>f'(0)=t(1+0)^{t-1}-t=0$

Từ đó suy ra $\displaystyle f(i)$ cũng là một hàm đồng biến vì vậy

$\displaystyle f(i)>f(0)=(1 + 0)^t-(1 + t \times 0)=1-1=0$

Vậy trong trường hợp này: $\displaystyle A_2>A_1$
$\displaystyle \triangleright$ Trường hợp 2: Nếu $\displaystyle 0<t<1$ hoàn toàn tương tự với trường hợp 1, khi đó dễ thấy $\displaystyle f''(i)<0$ do đó $\displaystyle f'(i)$ là một hàm nghịch biến. Lại có $\displaystyle i>0$ cho nên:

$\displaystyle f'(i)<f'(0)=t(1+0)^{t-1}-t=0$

Từ đó suy ra $\displaystyle f(i)$ cũng là một hàm nghịch biến vì vậy

$\displaystyle f(i)<f(0)=(1 + 0)^t-(1 + t \times 0)=1-1=0$

Vậy trong trường hợp này: $\displaystyle A_2<A_1$

$\displaystyle \triangledown$

Ngoài cách sử dụng đạo hàm ta có thể sử dụng Định lý giá trị trung bình Lagrange để giải như sau:
Định lý giá trị trung bình
Cho $\displaystyle f:[a,b]\to \mathbb{R}$ là một hàm liên tục trên $\displaystyle [a,b]$ và khả vi trên $\displaystyle (a,b)$ . Khi đó tồn tại $\displaystyle c\in (a,b)$ sao cho:

$\displaystyle \frac{f(b)-f(a)}{b-a}=f'(c)$

Quay trở lại bài toán: Ta xét hàm $\displaystyle f(k)=(1+k)^t$ với $\displaystyle k\in (0,i)$ và $\displaystyle i>0$ . Theo định lý giá trị trung bình thì tồn tại một số $\displaystyle c \in (0,i)$ sao cho:

$\displaystyle \frac{f(i)-f(0)}{i-0}=f'(c) \iff \frac{(1+i)^t-1}{i}=t\times(1+c)^{t-1}$

$\displaystyle \Rightarrow(1+i)^t-1=i\times t\times(1+c)^{t-1}>t\times i \Rightarrow (1+i)^t>1+t\times i$

Điều trên đúng là do với $\displaystyle t>1$ và $\displaystyle c>0$ thì dễ thấy

$\displaystyle (1+c)^{t-1}>1 \iff (t-1)\times \ln{(1+c)}>\ln{1}=0$

Hiển nhiên đúng do hàm logarit nêpe $\displaystyle \ln{x}$ đồng biến với mọi $\displaystyle x>1$ .
Trường hợp $\displaystyle 0<t<1$ chứng minh hoàn toàn tương tự.

$\displaystyle \triangledown$

III. Kết luận:
Như vậy trong ngắn hạn nếu sử dụng lãi suất đơn thì khoản tiền đầu tư sẽ sinh lời nhiều hơn (so với dùng lãi kép) còn trong dài hạn thì sử dụng lãi suất kép thì khoản tiền đầu tư sẽ sinh lời nhiều hơn (so với dùng lãi đơn).

Mã CK	TC	Khớp lệnh		+/-
		Giá	KL

BUSINESS ADMINISTRATION

Home

Thứ Hai, 25 tháng 3, 2013

So sánh lãi đơn và lãi kép

Tổng số lượt xem trang